Study finds method to infinitely produce magnificent arrays of Islamic geometric designs

A scientist from the University of Sharjah in the United Arab Emirates has arrived at a new method that may help craftsmen to simulate and produce immeasurable numbers of stunning patterns of geometric Islamic designs traditionally used to grace mosques, madrasas, and palaces around the Muslim world.

Mostafa Zahri, a professor at Sharjah University's College of Sciences, draws on own research in which he demonstrates the elegance of these geometric designs, and provides a "new methodology (that) differs from all previous methods worldwide."

Throughout ages, scientists, craftsmen, and artists have traditionally used the drawing method to combine Islamic tiles and motifs, basically relying on grids constructed with a ruler and at least a pair of compasses.

"The largest class of Islamic design employs, in general, complex and symmetrical polygons, where, in each polygonal graph, the starting design is a cell in the form of a symmetrical shape" through which artists can create symmetrical rectangular, triangular, and circular designs with beautiful ornamental patterns, says Prof. Zahri.

The prevalent Islamic designs are the result of drawing and combing of shapes and patterns. "What I present in my research is an analytical method based on advanced mathematical functions. The output of these functions is somehow a design. Therefore, the concept based on drawing could be limited and the concept of using parametric function could offer an infinity of possibilities for creating Islamic geometric patterns."

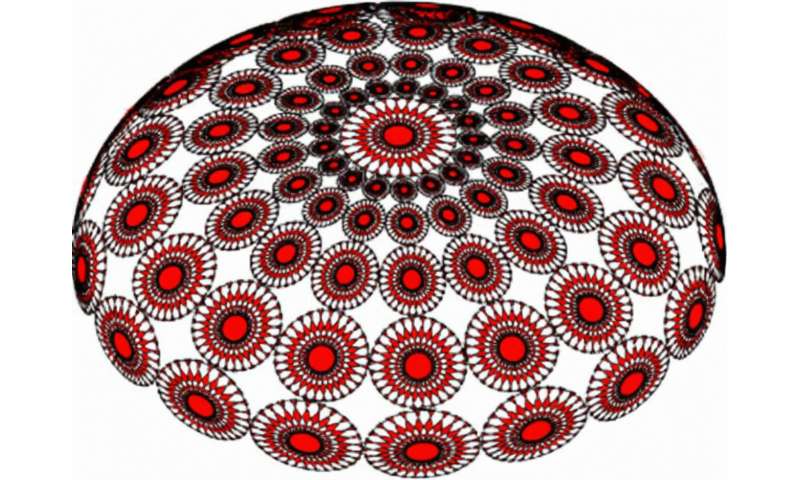
Prof. Zahri's research presents a new model for simulating an interesting class of Islamic design. "Based on periodic sequences on the one-dimensional manifolds and emerging numbers, he constructs "closed graphs with edges on the unit circle. These graphs build very nice shapes, leading to a symmetrical class of so-called Islamic geometric design patterns."

Prof. Zahri introduces mathematical equations to come up with multitudes of Islamic geometric patterns. "In our case, an Islamic design results from a predefined parameters combination. In other words, each design has a code containing the number of loops and the vertices. In this way, we can generate infinitely many Islamic designs."

The new methodology has spawned fresh and simple techniques not only to draw a plethora of a variety of astounding Islamic designs, but also to integrate the geometrical frameworks into mathematics education which Prof. Zahri is also using "for motivating students to increase their interest in studying sciences, especially mathematics."

"This mathematical project explains and gives an analytical mathematical approach to the geometry used for constructing unit cells and the different types of arrangements. Moreover, it allows, in an easy way, the production of many similar and more complicated designs," he writes.

"Furthermore, generalizing the proposed work project to curved surface inputs is an interesting avenue for future research, particularly for developing similar and easy models to make mathematics more attractive for students, artists, scientists, and non-mathematician researchers."

Geometry in Islamic civilization is not merely a discipline for mathematicians. Islamic craftsmen, artists and scientists turned geometry into an art form of mathematical elegance to draw remarkable Islamic patterns to adorn places of worship with geometric designs of magnificent proofs and shapes, mixing history, culture, art, and mathematics.

Islamic artists and craftsmen transformed geometry into an art form because they were not allowed to draw representations of humans to adorn their places of worship. However, interest in this geometric artform is today not confined to holy places. Demand to embellish palaces and monuments with Islamic geometrical designs is high across the Arab and Muslim world, and often worldwide.

"The Islamic arts use complex geometric patterns and shapes. In wood for ornamental patterns, in bricks of buildings, in brass for decorations, paper, tiling, plaster, glass, etc.," says Prof. Zahri, adding: "Islamic Design could be found mainly in three distinct geometrical patterns: rectangular Kufic fonts, the arabesque shapes, and polygonal designs."

Prof. Zahri notes: "Islamic architecture is renowned for its intricate use of geometric patterns as decorative elements in various structures like domes, minarets, courtyards, mosques, and public buildings. These remarkable patterns are the product of planar and spatial geometry, resulting in polygonal shapes.

Mathematically, precise calculations create diverse unit cells, which serve to generate a vast number of shapes and designs. Through a combination of overlapping and non-overlapping arrangements, applying these mathematical principles gives rise to both symmetrical and pseudo-symmetrical Islamic designs."

Prof. Zahri's main object is to put his model to practical use by applying "existent designs and finding scientific methods for generating other unique shapes. The main goal is to demonstrate to students how useful geometry is. And how beautiful mathematics is. From the industrial point of view, we can code these designs to present them to a special market."

Since publishing his research, Prof. Zahri's desire has been to popularize his model and make it accessible to students, peer scholars, and the public to help them draw lines and circles to produce patterns that will connect them to their heritage.

Prof. Zahri hopes that his research and geometric frameworks will boost interest in Islamic geometric heritage. He notes that so far artists and scientists have mostly been concentrating on replicating past design patterns with little room for creativeness and innovation.

Using the geometrical properties of connected and closed graphs with vertices on the unit circle, Prof. Zahri's mathematical approach dwells on the modeling of an interesting class of geometric patterns in Islamic design.

"The symmetries of vertices on the one-dimensional manifold leads to the construction of two-dimensional planar patterns, which are in the literature well known as a part of Islamic design. The resulting designs define beautiful fine arts and are, in general, expressed using basic mathematical transformations," he says.

Prof. Zahri describes his study as a harbinger of more solid research in the future in a hitherto sparsely investigated artistic discipline. "My research so far," he says, "is merely a starting point for further research to come up with models and frameworks of other classes of more Islamic geometric designs drawing on advanced techniques like those of Graph Theory."

In his paper, he writes: "A generalization of the proposed work to curved surface inputs is an interesting avenue for future research works, in particular for developing similar and easy models to contribute to making mathematics more attractive for students as well as for non-mathematician researchers."

More information:
Mostafa ZAHRI, Mathematical Modeling of a Class of Symmetrical Islamic Design, Symmetry (2019). DOI: 10.3390/sym11040517

Provided by University of Sharjah